Arithmetic Sequences and Sums

Sequence

A Sequence is a gear up of things (usually numbers) that are in order.

Sequence

Each number in the sequence is chosen a term (or sometimes "element" or "member"), read Sequences and Series for more than details.

Arithmetic Sequence

In an Arithmetic Sequence the difference betwixt i term and the next is a constant.

In other words, we just add the aforementioned value each time ... infinitely.

Example:

i, iv, vii, 10, thirteen, xvi, 19, 22, 25, ...

This sequence has a difference of 3 between each number.
The pattern is continued past adding 3 to the last number each fourth dimension, similar this:

arithmetic sequence 1,4,7,10,

In General we could write an arithmetics sequence like this:

{a, a+d, a+2d, a+3d, ... }

where:

  • a is the first term, and
  • d is the deviation between the terms (chosen the "common deviation")

Case: (continued)

1, four, 7, ten, 13, xvi, 19, 22, 25, ...

Has:

  • a = 1 (the get-go term)
  • d = three (the "mutual divergence" between terms)

And nosotros get:

{a, a+d, a+2d, a+3d, ... }

{1, 1+3, 1+2×3, 1+3×iii, ... }

{i, 4, 7, ten, ... }

Rule

We tin can write an Arithmetics Sequence equally a rule:

10n = a + d(n−1)

(We use "n−1" because d is non used in the 1st term).

Example: Write a dominion, and calculate the 9th term, for this Arithmetics Sequence:

3, eight, xiii, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 betwixt each number.

arithmetic sequence 3,8,13,18

The values of a and d are:

  • a = three (the get-go term)
  • d = v (the "common difference")

Using the Arithmetic Sequence dominion:

10n = a + d(northward−1)

= 3 + 5(n−1)

= three + 5n − five

= 5n − 2

So the 9th term is:

x9 = five×nine − 2
= 43

Is that right? Cheque for yourself!

Arithmetic Sequences are sometimes chosen Arithmetic Progressions (A.P.'s)

Advanced Topic: Summing an Arithmetic Series

To sum upwards the terms of this arithmetic sequence:

a + (a+d) + (a+2d) + (a+3d) + ...

use this formula:

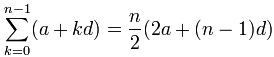
Sigma

What is that funny symbol? It is chosen Sigma Notation

Sigma (called Sigma) means "sum up"

And below and higher up it are shown the starting and catastrophe values:

Sigma Notation

It says "Sum up n where northward goes from 1 to 4. Answer=10

Here is how to use it:

Case: Add up the first 10 terms of the arithmetic sequence:

{ 1, 4, 7, ten, 13, ... }

The values of a, d and north are:

  • a = 1 (the first term)
  • d = 3 (the "mutual difference" between terms)
  • n = 10 (how many terms to add together up)

So:

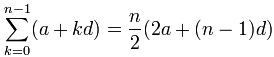
Sigma

Becomes:

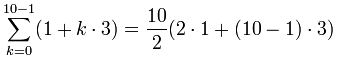
Sigma

= 5(2+9·3) = v(29) = 145

Check: why don't yous add up the terms yourself, and run across if information technology comes to 145

Footnote: Why Does the Formula Work?

Permit's see why the formula works, because we get to use an interesting "trick" which is worth knowing.

First, we will call the whole sum "Southward":

S = a + (a + d) + ... + (a + (n−2)d) + (a + (n−1)d)

Next, rewrite S in reverse order:

Due south = (a + (n−1)d) + (a + (northward−two)d) + ... + (a + d) + a

Now add together those two, term by term:

S = a + (a+d) + ... + (a + (north-2)d) + (a + (n-one)d)
Due south = (a + (northward-i)d) + (a + (north-two)d) + ... + (a + d) + a
2S = (2a + (northward-1)d) + (2a + (northward-1)d) + ... + (2a + (north-1)d) + (2a + (north-1)d)

Each term is the same! And in that location are "north" of them so ...

2S = northward × (2a + (n−1)d)

At present, just divide by 2 and we get:

S = (n/ii) × (2a + (n−i)d)

Which is our formula:

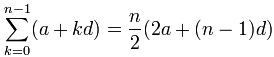
Sigma